Untuk mencari penyelesaian persamaan kuadrat, terdapat beberapa metode yang dapat digunakan, diantaranya yaitu faktorisasi, kuadrat sempurna, dan menggunakan rumus ABC. Berikut penjelasan mengenai beberapa metode untuk mencari penyelesaian persamaan kuadrat.
1. Faktorisasi / Pemfaktoran
adalah suatu metode dalam menentukan akar-akar dengan mencari nilai yang jika dikalikan maka akan menghasilkan nilai lain. Terdapat tiga bentuk persamaan kuadrat (PK) dengan faktorisasi akar-akar yang berbeda, yaitu:
Berikut contoh soal mengenai penggunaan metode faktorisasi pada persamaan kuadrat.
Selesaikan persamaan kuadrat \(5x^2+13x+6=0\) menggunakan metode faktorisasi.
Penyelesaian:
\(5x^2+13x+6=0\).
\(5x^2+10x+3x+6=0\).
\(5x(x + 2) + 3(x + 2) = 0\)
\(5x + 3)(x + 2) = 0 \)
\(5x = -3\) atau \(x = -2\)
Jadi penyelesaiannya adalah \(𝑥 = \frac{−
3}{5}\) atau \(𝑥 = −2\)
2. Kuadrat Sempurna
Bentuk kuadrat sempurna merupakan bentuk persamaan kuadrat yang menghasilkan bilangan
rasional.
Hasil dari persamaan kuadrat sempurna umumnya menggunakan rumus sebagai berikut:
\((x+p)^2\)= \(x^2 + 2px +p^2\)
Penyelesaian umum dari persamaan kuadarat sempurna ialah sebagai berikut:
\((x+p)^2\)= \(x^2 + 2px +p^2\) dengan pemisalan \((x+p)^2 = q\) , maka:
\((x+p)^2 = q\)
\(x+p = ± q \)
\(x = -p ± q\)
Berikut contoh soal mengenai penggunaan metode persamaan sempurna.
Selesaikan persamaan \(x^2
+ 6x + 5 = 0\) menggunakan metode persamaan kuadrat sempurna !
Penyelesaian:
\(x^2
+ 6x +5 = 0\)
\(x^2
+ 6x = -5\)
Langkah selanjutnya yaitu tambahkan satu angka di ruas kanan dan kiri hingga dapat
membentuk kuadrat sempurna
\(x^2
+ 6x + 9 = -5 + 9\)
\(x^2 + 6x + 9 = 4\)
\((x+3)^2
= 4\)
\((x+3)\)= \(\sqrt[]{4}\)
\(x = -3 ± 2\)
Jadi, hasil akhirnya adalah \(x = -1\) atau \(x = -5\)
3. Rumus Kuadrat ABC
Rumus abc merupakan alternatif pilihan ketika persamaan kuadrat sudah tidak bisa diselesaikan
dengan metode faktorisasi maupun kuadrat sempurna.
Berikut rumus formula abc pada persamaan kuadrat \(ax^2
+bx + c = 0\).
Menyusun Persamaan Kuadrat baru
Menyusun persamaan kuadrat baru dari akar-akar yang telah diketahui sebelumnya.
Berikut beberapa cara yang dapat digunakan untuk menyusun persamaan kuadrat baru.
1. Menyusun persamaan jika telah diketahui akar-akarnya
Jika sebuah persamaan memiliki akar 𝑥1 dan 𝑥2
, maka persamaan yang dapat dibentuk dari akar- akar tersebut dinyatakan dalam bentuk
(𝑥 - 𝑥1 )(𝑥 - 𝑥2 ) = 0
Contoh:
Tentukan persamaan kuadrat dimana akar-akarnya diantaranya -2 dan 3.
Penyelesaian: 𝑥1= −2 dan 𝑥2 = 3
\((𝑥 − (−2))(𝑥 − 3) =0 \)
\((𝑥 + 2)(𝑥 - 3)\)
\(x^2
− 3x + 2x – 6 = 0 \)
\(x^2
– x – 6 = 0\)
Jadi, persamaan kuadrat dari akar-akar tersebut adalah \(x^2 – x – 6 = 0\)
2. Menyusun persamaan kuadrat jika jumlah serta hasil kali akar diketahui
Jika akar-akar persamaan kuadratnya merupakan jumlah dan hasil kali 𝑥1 dan 𝑥2 yang telah
diketahui, maka persamaan kuadratnya dapat diubah dalam bentuk sebagai berikut.
\(x^2\) – (𝑥1 + 𝑥2
)𝑥+(𝑥1𝑥2
) = 0
Contoh:
Tentukan persamaan kuadrat yang memiliki akar 3 dan \(\frac{-1}{2}\)
Penyelesaian:
𝑥1 = 3 dan 𝑥2 = \(\frac{1}{2}\)
𝑥1+ 𝑥2 = 3 + \(\frac{-1}{2}\)= \(\frac{6}{2}\) − \(\frac{-1}{2}\) = \(\frac{5}{2}\)
𝑥1. 𝑥2 = 3 ( \(\frac{-1}{2}\) ) = \(\frac{-3}{2}\)
Sehingga, persamaan kuadratnya menjadi :
\(x^2\) – (𝑥1 + 𝑥2 )𝑥+(𝑥1𝑥2 ) = 0
\(x^2\) – \(\frac{5}{2}\)𝑥 − \(\frac{3}{2}\) = 0 (masing-masing ruas dikali 2)
\(2x^2
– 5x – 3 = 0\)
Jadi, persamaan kuadrat dari akar 3 dan \(\frac{-1}{2}\) adalah \(2x^2 – 5x – 3 = 0\)
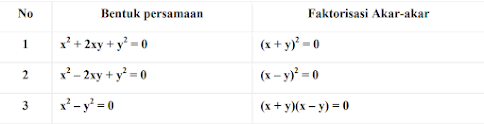

Tidak ada komentar:
Posting Komentar